
Esempio di una sezione trasversale della superficie K3 in 3-spazio, simile a un modello Utah State University e University of Missouri-St. I matematici di Louis erano soliti esaminare le dualità delle stringhe tra la teoria F e la teoria eterotica in otto dimensioni. Credito:USU
In poche parole, la teoria delle stringhe è un metodo proposto per spiegare tutto. In realtà, non c'è niente di semplice. La teoria delle stringhe è un quadro teorico della fisica che descrive unidimensionale, oggetti fibrosi vibranti chiamati "corde, " che si propagano nello spazio e interagiscono tra loro. Pezzo per pezzo, le menti energetiche stanno scoprendo e decifrando le stringhe fondamentali dell'universo fisico usando modelli matematici. Tra questi intrepidi esploratori ci sono i matematici della Utah State University Thomas Hill e il suo mentore di facoltà, Andreas Malmendier.
Con il collega Adrian Clingher dell'Università del Missouri-St. Louis, il team ha pubblicato i risultati su due rami della teoria delle stringhe nell'articolo, "La dualità tra la teoria del F e la stringa eterotica in D =8 con due linee di Wilson, "il 7 agosto, Edizione online 2020 di Lettere in Fisica Matematica. Il lavoro dei ricercatori dell'USU è sostenuto da una sovvenzione della Simons Foundation.
"Abbiamo studiato una famiglia speciale di superfici K3:compatte, superfici complesse connesse di dimensione 2, che sono importanti strumenti geometrici per comprendere le simmetrie delle teorie fisiche, "dice Collina, che si è laureato presso l'Honours Program dell'USU con una laurea in matematica nel 2018 e ha completato un master in matematica la scorsa primavera. "In questo caso, stavamo esaminando una dualità di stringa tra la teoria F e la teoria delle stringhe eterotiche in otto dimensioni".
Hill afferma che il team ha dimostrato che le superfici K3 che hanno studiato ammettono quattro modi unici per suddividere le superfici come fibrazioni ellittiche Jacobiane, formazioni di fibre toroidali. I ricercatori hanno costruito equazioni esplicite per ciascuna di queste fibrazioni.
"Una parte importante di questa ricerca riguarda l'identificazione di alcuni blocchi geometrici, chiamati 'divisori, " all'interno di ogni superficie K3, " dice. "Usando questi divisori, le informazioni geometriche cruciali vengono quindi codificate in un grafico astratto".
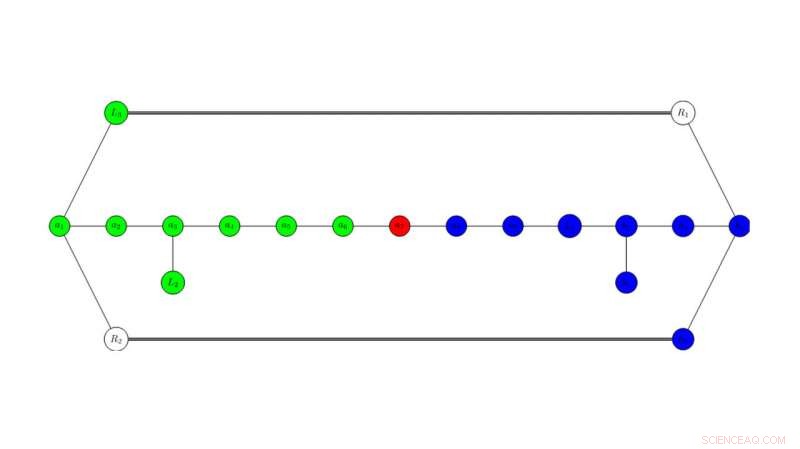
Utilizzando un grafico astratto, I ricercatori della Utah State University identificano i divisori all'interno di ogni superficie K3 per esaminare varie simmetrie. Le diverse fibrazioni ellittiche jacobiane corrispondono a colori specifici di un sottoinsieme connesso dei nodi del grafo. Le simmetrie del grafo e le possibili colorazioni dei nodi sono cruciali per comprendere le simmetrie delle teorie fisiche sottostanti. Credito:Malmendier/Collina, USU
Questo processo, Hill dice, consente ai ricercatori di studiare le simmetrie delle teorie fisiche sottostanti dimostrate dal grafico.
"Puoi pensare a questa famiglia di superfici come una pagnotta e ogni fibrazione come una 'fetta' di quella pagnotta, "dice Malmendier, professore associato presso il Dipartimento di Matematica e Statistica dell'USU. "Esaminando la sequenza delle fette, possiamo visualizzare, e capire meglio, tutta la pagnotta».
L'impresa descritta nel documento, lui dice, rappresenta ore di scrupoloso lavoro "carta e matita" per dimostrare i teoremi di ciascuna delle quattro fibrazioni, seguito spingendo ogni teorema attraverso formule algebriche difficili.
"Per l'ultima parte di questo processo, abbiamo utilizzato il software Maple e il pacchetto specializzato di geometria differenziale sviluppato presso l'USU, che ha semplificato i nostri sforzi di calcolo, "dice Malmendier.