Il 5 gennaio Rosa Winter conseguirà il dottorato in geometria aritmetica. Ha ricercato soluzioni di equazioni che definiscono le cosiddette 'superfici del Pezzo." "Mi piace la geometria perché posso immaginare e disegnare le forme e gli oggetti, " dice Winter. "Questo rende la matematica astratta più tangibile."

In matematica, a volte è utile studiare equazioni astratte usando oggetti geometrici, come i cerchi, sfere, ottaedri, o anche oggetti di dimensioni superiori. Il campo che collega la geometria con le equazioni astratte è chiamato geometria aritmetica. dottorato di ricerca la candidata Rosa Winter ha applicato questo specifico tipo di geometria nella sua tesi.

Superfici di disegno

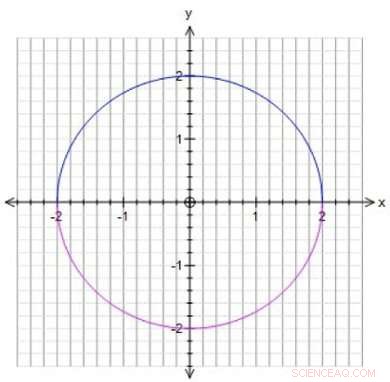
Le equazioni matematiche possono definire oggetti geometrici, il che significa che è possibile studiare le soluzioni di quelle equazioni usando la geometria. Per esempio, se vuoi sapere quali numeri puoi inserire per rendere x^2+y^2 uguale a 4, puoi disegnare tutti i punti (soluzioni) per i quali x^2+y^2=4. Ne risulta un cerchio di raggio 2, che mostra, Per esempio, che il punto x=2, y=0 è una soluzione. Puoi anche cercare soluzioni specifiche, come punti sul cerchio dove xey sono frazioni (1/3rd, 1/5, ma anche, 0, 2, eccetera.). Queste soluzioni frazionarie sono chiamate punti razionali. Winter ha studiato i punti razionali sulle superfici. "Le superfici sono sempre bidimensionali, anche se vivono in otto dimensioni, " dice Winter. "Il che significa che posso disegnare superfici, rendendo la matematica astratta più intuitiva per me."

Domanda da un milione di dollari

Trovare punti razionali su oggetti geometrici è raramente facile. Questo è mostrato, Per esempio, dalla cosiddetta "congettura di Birch e Swinnerton-Dyer". Questa congettura matematica non ancora dimostrata fa parte dei problemi del Millennium Prize. Il Clay Mathematics Institute assegna un milione di dollari per una corretta soluzione a uno qualsiasi di questi problemi. La congettura riguarda i punti razionali su curve ellittiche. come cerchi, le curve ellittiche sono oggetti geometrici definiti da determinate equazioni. Quando li disegni, sembrano linee curve. Inverno:"Anche sulle curve ellittiche, di cui sappiamo abbastanza, non è facile determinare l'insieme dei punti razionali."

Superfici Del Pezzo

Sfortunatamente, Winter non ha raccolto il milione di dollari durante il suo dottorato. ricerca. Non ha lavorato su punti razionali su curve ellittiche, ma su superfici cosiddette 'del Pezzo di grado 1." Winter:"Dal punto di vista geometrico, queste non sono le più difficili, superfici più complicate ma tengono ancora questioni matematiche senza risposta." Ha mostrato per parte di questa famiglia di superfici che contiene un numero infinito di punti razionali che non si raggruppano; possono essere trovati sparsi intorno alle superfici. Se i punti razionali fossero visibili come puntini rossi e potresti camminare su una superficie così del-Pezzo, vedresti punti razionali rossi ovunque guardi.

Da settembre, Winter ha lavorato come postdoc presso il Max Planck Institute for Mathematics in the Sciences di Lipsia. Qui impara, tra l'altro, come applicare la geometria e la matematica astratta in altre scienze, come la biologia e la fisica.