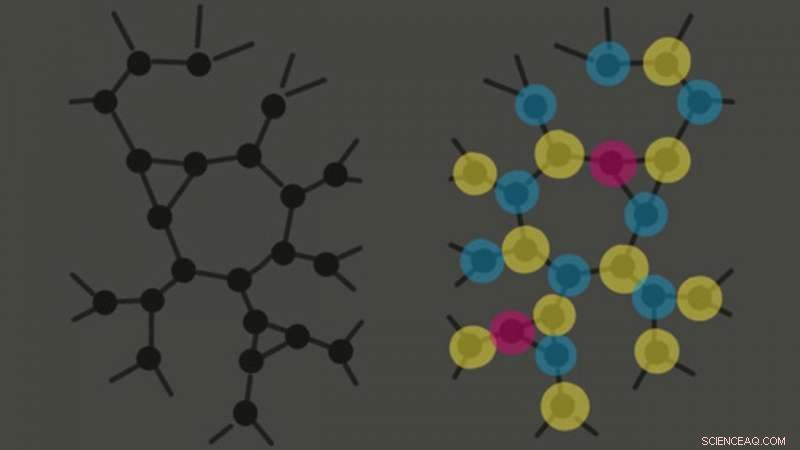
Gli algoritmi possono distinguere questi due grafici? Il grafico uniforme a sinistra è difficile da distinguere dalla soluzione piantata a destra. Credito:Jess Banks, presentazione riassuntiva alla Conferenza 2021 sulla teoria dell'apprendimento
Nell'informatica, il problema della colorazione dei grafici è un classico. Ispirato dal problema della colorazione delle mappe, chiede:Data una rete di nodi collegati da collegamenti, qual è il numero minimo di colori necessari per colorare ogni nodo in modo che nessun collegamento colleghi due dello stesso colore? Per piccoli numeri di colori e collegamenti, cercare una soluzione è semplice:basta provare tutte le possibili combinazioni. Ma man mano che i collegamenti aumentano, il problema diventa più limitato, finché, se ci sono troppi collegamenti e non abbastanza colori, non può esistere alcuna soluzione.
"Poi ci sono queste affascinanti zone intermedie dove probabilmente c'è una soluzione, ma è molto difficile da trovare, e un altro dove probabilmente non c'è, ma è difficile dimostrare che non c'è, " dice il poliedrico Cris Moore, un professore residente a SFI. Ciò significa che gli algoritmi di risoluzione dei problemi convenzionali non possono trovarli, lui dice. Se si inizia con una colorazione casuale, Per esempio, e inizia a capovolgere i colori dei nodi, non troverà una di queste soluzioni nascoste.
In un nuovo documento presentato alla Conferenza 2021 sulla teoria dell'apprendimento, Moore ei suoi collaboratori descrivono un nuovo modo di costruire problemi con tali soluzioni nascoste. Il gruppo comprende il matematico Jess Banks, un ex stagista universitario e post-diploma di SFI che ora sta perseguendo un dottorato di ricerca. presso l'Università della California-Berkeley.
Si avvicinano al problema interpretando una sorta di avvocato del diavolo matematico. Invece di risolvere i problemi, si compongono di nuovo, complicati, con soluzioni nascoste all'interno. "Ci togliamo il cappello bianco del risolutore, il cercatore di soluzioni, e indossiamo il cappello nero della persona che progetta problemi complicati, quasi come la crittografia, " dice Moore. "La soluzione è nascosta."
I ricercatori hanno escogitato un modo sottile per nascondere le soluzioni, dice Moore. E quando affidano questi problemi ad algoritmi di risoluzione dei problemi, gli algoritmi risultano vuoti. "Se possiamo creare problemi che molti algoritmi non possono risolvere, o anche dire se c'è una soluzione, "dice Moore, "allora abbiamo una forte evidenza che abbiamo localizzato la zona in cui questi problemi sono difficili".
Il documento include un teorema che dimostra che più famiglie di algoritmi non riescono a trovare soluzioni a questi problemi generati. Ciò significa che i ricercatori sono più vicini che mai all'identificazione del confine di transizione di fase di questa zona "difficile" in cui è difficile trovare soluzioni o dimostrare che non ce ne sono.
Moore afferma che lo sforzo in corso per identificare con precisione i problemi è nato da congetture in fisica che chiedono come cambiano i sistemi man mano che diventano più vincolati.
"La nostra avventura, " lui dice, "è stato trasformare queste congetture e questi calcoli in fisica in dimostrazioni matematiche". E l'unico modo per continuare a spingere il campo in avanti, lui dice, è fare appello ai punti di forza sovrapposti degli strumenti della matematica, fisica, e informatica.