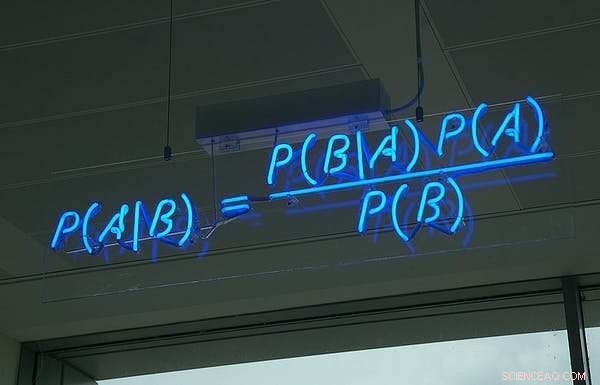
Teorema di Bayes, in neon, nell'ufficio della società di software britannica HP Autonony. Credito:Wikimedia Commons, CC BY
Le catastrofiche inondazioni della costa orientale dell'Australia sono state descritte dal premier del NSW come "un evento su 1.000 anni, un termine che ha creato molta confusione.
Spiegazioni lunghe che questi termini non sono gli stessi di "che si verificano a distanza di 1.000 anni" o "una volta ogni 1.000 anni" hanno solo aggiunto confusione.
La spiegazione più semplice è che il vero significato di "uno su 1.000 anni" è "avere una probabilità dello 0,1 per cento in un dato anno" (1 su 1.000), il che solleva la domanda:perché le persone non lo dicono semplicemente?
Il motivo principale è che questi termini risalgono a un'epoca in cui la maggior parte delle persone non pensava in termini di probabilità e anche coloro che lo facevano erano confusi su come funzionavano. In questi giorni interagiamo continuamente con le probabilità.
Le previsioni meteorologiche giornaliere includono una percentuale di probabilità di pioggia e le previsioni a lungo termine danno le probabilità di precipitazioni superiori o inferiori alla media secondo i cicli di El Nino e La Nina.
I mercati finanziari scommettono sulle probabilità o sui movimenti dei tassi di interesse. Statistica e probabilità vengono insegnate ai bambini a scuola.
Ma questo è uno sviluppo abbastanza recente.
Fino al 17° secolo, anche i concetti più elementari della teoria della probabilità erano sconosciuti. La gente pensava al destino e alla fortuna come essenzialmente inconoscibili. Anche i giocatori d'azzardo non capivano le probabilità.
La nascita della probabilità
In effetti, fu una richiesta di un amico giocatore d'azzardo intorno al 1654 che spinse il filosofo e matematico francese Blaise Pascal a sviluppare i concetti di base della probabilità con il collega matematico Pierre de Fermat.
(Pascal usò anche l'idea per sviluppare la "scommessa di Pascal" usata per dimostrare l'utilità di credere in Dio. L'idea è che se Dio esiste, i credenti saranno ricompensati con la beatitudine eterna. In caso contrario, rinunceranno a un numero limitato di piaceri terreni mentre vivo. Non importa quanto piccola sia la probabilità che Dio esista, il vantaggio di credere in Dio si rivela infinito mentre il costo è finito.)
La comprensione si è sviluppata lentamente. Non è stato fino alla metà del 18° secolo che il pastore inglese Thomas Bayes è stato accreditato dello sviluppo più importante del campo.
Lo strumento lasciato in eredità da Bayes
Nella sua interpretazione moderna, il teorema di Bayes ci fornisce i mezzi per rivedere la nostra visione della probabilità di un evento alla luce delle prove su ciò che è appena accaduto.
Se qualcosa è appena accaduto o meno viene esplicitamente inserito nel ricalcolo insieme a valutazioni aggiornate della probabilità che ciò sia importante.
Fino a Bayes, la maggior parte delle probabilità erano calcolate come se non cambiassero, come la probabilità di ottenere "testa" quando si lancia una moneta. Tali probabilità potrebbero essere utilmente descritte come "una su 1.000 anni" o "in media, ogni secondo lancio".
Ma la probabilità di una grave inondazione cambia nel tempo al variare del rapporto tra le componenti che compongono il sistema meteorologico. Se si è verificata un'alluvione ci fornisce prove di tale cambiamento.
Questo non rende più utile fare riferimento a una grave inondazione come evento "uno ogni x anni".
È passato molto tempo da quando abbiamo cambiato la terminologia di una volta ogni-così-tanti anni, ma in cosa? La risposta sembra semplice, anche se i dettagli saranno complicati.
In primo luogo, dobbiamo convertire le vecchie misure in scale di gravità, simili a quelle utilizzate per i cicloni e i terremoti, ma specifiche per ciascun bacino.
Fatto ciò, la probabilità di un evento di data gravità può essere stimata sulla base dell'esperienza storica e aggiornata alla luce di nuove evidenze.
Come si applicherebbe nel caso di un evento come l'alluvione del Lismore?
La descrizione iniziale "uno in 1.000 anni" significa che un tale evento sarebbe estremamente improbabile se la vecchia relazione fosse mantenuta.
Usando il teorema di Bayes, aggiorneremmo quella iniziale su 1.000 probabilità sulla base di informazioni aggiornate sulla possibilità che le relazioni sottostanti stiano cambiando, producendo nuove probabilità annuali ogni anno.
Ecco come funziona l'apprendimento automatico e come vengono aggiornate le quote mediche e assicurative. Purtroppo, le probabilità riviste supereranno quasi sicuramente una su 1.000.