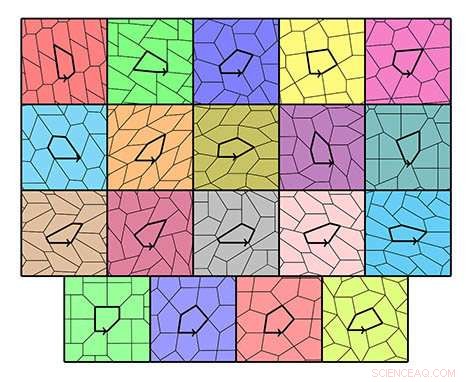
I 15 tipi di piastrelle pentagonali e i loro 4 tipi specifici © Michael Rao, Laboratoire d'informatique du parallelélisme. Credito:CNRS/Inria/ENS Lyon/Université Claude Bernard Lyon
La piastrellatura dell'aereo con un unico modello è un problema matematico che ha interessato gli umani fin dall'antichità, in particolare per la qualità estetica delle tessere dei mosaici o delle piastrelle. Uno dei problemi irrisolti in questo campo che dal 1918 sconcertava la comunità scientifica è stato ora definitivamente risolto grazie a Michaël Rao del Laboratoire d'informatique du parallélisme (CNRS/Inria/ENS de Lyon/Université Claude Bernard Lyon 1). Usando strumenti informatici è stato in grado di dimostrare che ci sono solo 15 modelli a cinque lati che possono affiancare l'aereo. La ricerca è ora disponibile su Arxiv sito web.
Esistono numerose soluzioni per rivestire un pavimento con un'unica forma, come triangoli, piazze, rettangoli, esagoni, ecc. La ricerca esaustiva di tutte le forme convesse che possono affiancare il piano - una forma con angoli inferiori a 180° che può coprire un'intera parete senza sovrapporsi - è stata avviata da Karl Reinhardt durante la sua tesi nel 1918. Ha mostrato che tutti i triangoli e i quadrilateri possono affiancare il piano, ma che c'erano solo 3 tipi di esagoni che potevano farlo, e che un poligono con sette lati o più non potrebbe farlo. Restava aperta solo la questione dei pentagoni.
15 tipi di pentagoni sono stati scoperti dal 1918 al 2015 come parte di una ricerca singolare:iniziata da Reinhardt nel 1918, ha attraversato una serie di colpi di scena, come nuove scoperte di matematici dilettanti, fino all'annuncio mediatizzato nel 2015 di un nuovo 15° modulo 30 anni dopo il 14°. Eppure la comunità scientifica non era ancora in grado di determinare se esistessero altre forme di pentagoni che potessero affiancare l'aereo.
Michael Rao, un ricercatore CNRS presso il Laboratoire d'informatique du parallélisme (CNRS/Inria/ENS Lyon/Université Claude Bernard Lyon 1), ha ora definitivamente dimostrato che c'è solo una serie finita di famiglie di pentagoni da prendere in considerazione. Rao ha utilizzato un programma software per generare tutte le possibilità, e ha mostrato che 371 famiglie di pentagoni potrebbero potenzialmente affiancare l'aereo. Ha quindi testato ciascuna di queste famiglie utilizzando un altro programma, e ha dimostrato che solo 19 tipi di pentagoni soddisfacevano le condizioni per gli angoli e le lunghezze dei lati richieste per piastrellare il piano. Tra questi 19 tipi, 15 corrispondeva a tipi già noti, e gli altri quattro si sono rivelati casi particolari di questi 15 tipi. Di conseguenza, solo 15 tipi di tessere possono affiancare l'aereo.
Rao è riuscito a risolvere un problema secolare con la sua metodologia, e per aprire nuove prospettive. Tutte queste tessere convesse possono affiancare periodicamente il piano (cioè, le tessere si ripetono all'infinito). Eppure non è ancora noto se esista una piastrella che consenta la piastrellatura non periodica. Fortunatamente la maggior parte di queste tecniche può essere utilizzata anche per poligoni non convessi, e potrebbe quindi servire come base per risolvere un altro problema nel campo della piastrellatura, meglio conosciuto come "Problema Einstein" (dal tedesco "ein stein").