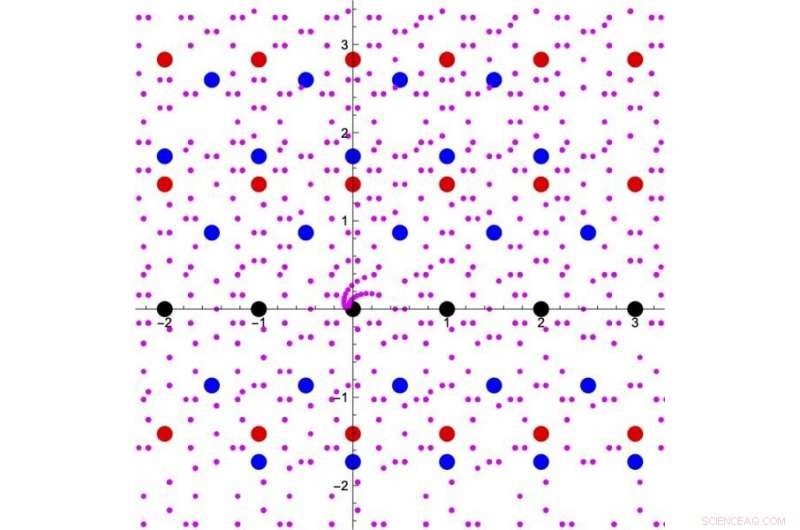
Figura 1. Estensione del concetto di "numeri" integrali. I punti neri sono gli interi ordinari mostrati in un piano complesso. L'aggiunta o la moltiplicazione di qualsiasi coppia di punti neri finisce con un altro punto nero. Tutti i punti rossi e blu in questa figura sono soluzioni di alcune equazioni quadratiche con coefficienti interi. I punti viola sono soluzioni di alcune equazioni quartiche con coefficienti interi. Così, possiamo pensare a quei punti anche come parte di "numeri". Le operazioni di addizione e moltiplicazione tra punti neri o rossi rimangono all'interno dei "numeri" mostrati nei punti neri o rossi, e similmente, quelle operazioni di punti nero-rosso-blu-o-viola rimangono all'interno dei "numeri" in punti nero-rosso-blu-o-viola. In questo modo, è possibile espandere gradualmente l'insieme dei "numeri" integrali. Attestazione:Kavli IPMU
Una collaborazione tra un matematico e un fisico ha mostrato che le forme modulari associate alle curve ellittiche con moltiplicazioni complesse sono espresse in termini di osservabili nella teoria delle superstringhe.
Il concetto di numeri può essere esteso da interi e numeri razionali per includere tutti i numeri reali e i numeri complessi, tutto in una volta. Ma è anche possibile estendere il concetto gradualmente, sommando a poco a poco le radici dei polinomi con coefficienti di numero razionale (come la radice quadrata di 2 e la radice quadrata di 3) (Figura 1). Questa classe speciale di numeri complessi viene chiamata "numeri". I dettagli precisi di come il concetto di numeri può essere esteso è stato considerato come uno dei temi importanti nella teoria dei numeri.
Per diversi decenni, i ricercatori hanno cercato di affrontare e comprendere questo problema. Si potrebbe specificare un oggetto geometrico tramite equazioni usando prima i "numeri", e poi considerare l'insieme dei punti nell'oggetto geometrico i cui valori sono i "numeri". Man mano che il concetto di numero si estende gradualmente, e l'insieme dei "numeri" si espanse, sempre più punti nell'oggetto geometrico vengono contati (Figura 2). L'idea è che il modo in cui aumenta il numero di punti nell'oggetto geometrico farà luce su come si espande l'insieme di "numeri". Per di più, questa informazione del tasso di crescita del numero di punti nell'oggetto geometrico è impacchettata in una funzione chiamata trasformata di Mellin inversa della funzione L, che è una funzione che contiene l'informazione di quanto velocemente cresce il numero di punti in un oggetto geometrico man mano che si estende il concetto di numeri. Questa funzione doveva essere una forma modulare, una funzione che rimane invariante in determinate operazioni. Questa congettura è nota come congettura di Langlands.
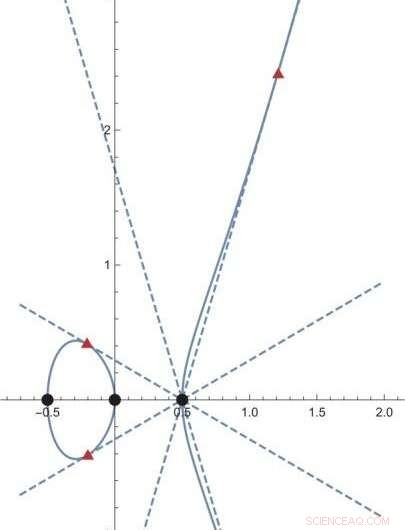
Figura 2. Un oggetto geometrico dato da y^2 =4 x^3 - x è mostrato da una sottile curva blu. In questo oggetto, i tre punti neri hanno i loro valori negli interi ordinari. D'altra parte, i tre punti nei triangoli rossi hanno i loro valori in un insieme più esteso di "numeri" (le coordinate x sono della forma (p+q sqrt{2}) con numeri razionali peq; le coordinate y sono più complicate) . Man mano che il concetto di "numeri" viene esteso, il numero di punti con i loro valori nei "numeri" aumenta, anche per un dato oggetto geometrico. Attestazione:Kavli IPMU
Kavli Institute for the Physics and Mathematics of the Universe (Kavli IPMU) Professore associato e teorico delle particelle Taizan Watari e ricercatore di geometria aritmetica presso la Middle East Technical University Northern Cyprus Campus e Kavli IPMU Visiting Scientist Satoshi Kondo ha osato chiedere perché tali funzioni sono invarianti in determinate operazioni.
Nella teoria delle stringhe, è noto che una classe di osservabili (a) sono invarianti rispetto alle operazioni (x) già citate. L'invarianza rispetto alle operazioni è una proprietà indispensabile nella costruzione teorica della teoria delle superstringhe. Così, i ricercatori hanno mostrato che le trasformate di Mellin inverse delle funzioni L degli oggetti geometrici (b) sono espresse in termini della suddetta classe di osservabili (a) nella teoria delle superstringhe con quegli oggetti geometrici impostati come spazi target. Di conseguenza, ne consegue che le funzioni contenenti le informazioni di come si estende il concetto di numeri, l'inverso Mellin trasforma, (b) dovrebbe essere invariante in determinate operazioni, che dovrebbero essere forme modulari, (x) per ragioni dal punto di vista della teoria delle superstringhe.
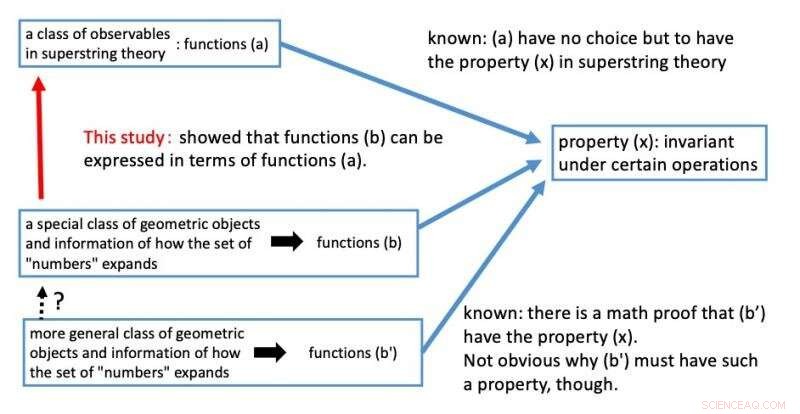
Figura 3. Riepilogo di questo studio. Credito:Kavli IPMU
Va notato che il risultato sopra si ottiene solo per la classe di oggetti geometrici chiamati curve ellittiche con moltiplicazioni complesse. Rimane aperta la questione se le funzioni per la classe più generale di oggetti geometrici (b) siano espresse in termini di osservabili nella teoria delle superstringhe (a).
I dettagli di questo studio sono stati pubblicati il 22 febbraio, 2019, in Comunicazioni in Fisica Matematica .