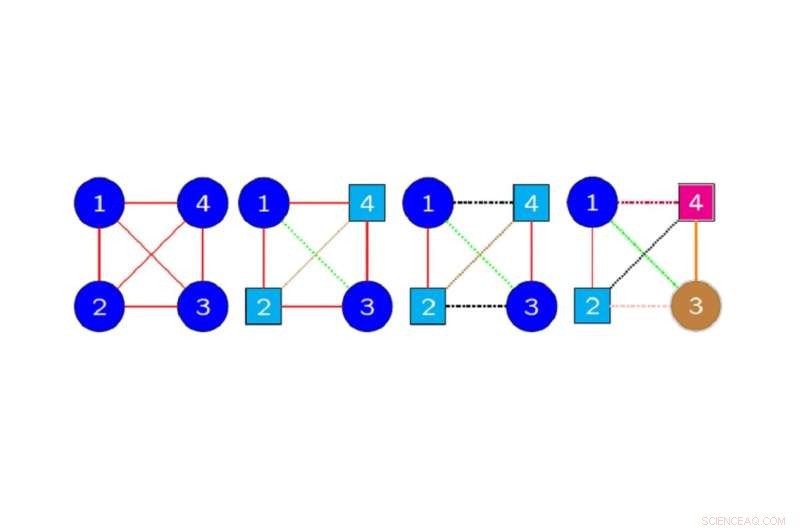
Esempi di grafici colorati che designano simmetrie di dati quadridimensionali:vertici e bordi dello stesso colore e forma in un grafico sono mappati tra loro da una permutazione di simmetria che preserva la struttura dei dati. Credito:Hideyuki Ishi, Università metropolitana di Osaka
Un team di ricerca internazionale guidato da scienziati dell'Università metropolitana di Osaka ha sviluppato un metodo per identificare le simmetrie nei dati multidimensionali utilizzando tecniche statistiche bayesiane.
Questo approccio statistico richiede calcoli complessi di integrali, che spesso sono considerati solo approssimazioni. Nel loro nuovo studio, il team di ricerca ha derivato con successo nuove formule integrali esatte. Le loro scoperte contribuiscono a migliorare l'accuratezza dei metodi per identificare le simmetrie dei dati, estendendone possibilmente le applicazioni ad aree di interesse più ampie, come l'analisi genetica.
Le simmetrie in natura rendono le cose belle; le simmetrie nei dati rendono efficiente la gestione dei dati. Tuttavia, la complessità dell'identificazione di tali modelli nei dati ha sempre infastidito i ricercatori. Gli scienziati della Osaka Metropolitan University ei loro colleghi hanno compiuto un passo importante verso il rilevamento delle simmetrie nei dati multidimensionali utilizzando le statistiche bayesiane. I loro risultati sono stati pubblicati in The Annals of Statistics .
La statistica bayesiana è stata al centro dell'attenzione negli ultimi anni a causa dei miglioramenti nelle prestazioni dei computer e delle sue potenziali applicazioni nell'intelligenza artificiale. La statistica bayesiana è un approccio statistico che, anche quando i dati sono insufficienti, ricava la probabilità che un evento si verifichi impostando prima una probabilità a priori e poi, ogni volta che si ottengono nuove informazioni, calcolando una probabilità a posteriori, un aggiornamento della probabilità a priori, che la accadrà l'evento. Il calcolo delle probabilità a posteriori richiede calcoli complessi di integrali e quindi è spesso considerato solo un'approssimazione.
Il team internazionale, tra cui il professor Hideyuki Ishi dell'Osaka Metropolitan University, il professor Piotr Graczyk dell'Università di Angers, il professor Bartosz Kołodziejek dell'Università di tecnologia di Varsavia e il compianto professor Hélène Massam dell'Università di York (Toronto) è riuscito a derivare nuove formule integrali esatte e nello sviluppo di un metodo per la ricerca di simmetrie nei dati multidimensionali utilizzando tecniche statistiche bayesiane.
Quando la quantità di dati da gestire aumenta, è necessario selezionare il modello ottimale da un vasto numero di modelli, rendendo difficile la risoluzione precisa del problema. Affrontando questa sfida, il team ha anche sviluppato un algoritmo efficiente per ottenere una soluzione approssimativa anche in questi casi.
Nelle parole del professor Ishi, "le simmetrie nei dati sono onnipresenti in un'ampia varietà di modelli. Una volta identificate le simmetrie, il numero di parametri necessari per visualizzare la struttura dei dati e il numero di campioni necessari per determinare i parametri, possono essere significativamente ridotto. In futuro, i risultati di questa ricerca dovrebbero contribuire all'analisi genetica, scoprendo cromosomi che hanno la stessa funzione in luoghi diversi". + Esplora ulteriormente