
Le catene montuose della Terra condividono le stesse caratteristiche universali. Diventano visibili quando la carta topografica (qui:le Alpi Liguri) viene trasformata in carta di cresta. (Fonte:IFJ PAN) Credito:Fonte:IFJ PAN
Le montagne hanno carattere. Il continuo gentile, colline ondulate e ampie valli dei Carpazi, Appalachi o parti inferiori delle Alpi contrastano fortemente con le vette svettanti, creste frastagliate e profonde gole degli alti monti Tatra e dei Pirenei, quali sono, a sua volta, diverso dall'inaccessibile, giganti himalayani o andini innevati, lungo le cui pendici scorrono lunghe lingue di ghiacciai invece che d'acqua. Sotto questa grande diversità, però, si trova una struttura sorprendentemente simile.
Utilizzando grafici e frattali, scienziati dell'Istituto di fisica nucleare dell'Accademia polacca delle scienze (IFJ PAN) di Cracovia hanno esaminato la struttura dei massicci del nostro pianeta. Gamme così diverse come le Alpi, i Pirenei, le montagne scandinave, i Monti Betici, l'Himalaya, le Ande, gli Appalachi, le montagne dell'Atlante e le Alpi meridionali sono andate tutte sotto la lente d'ingrandimento statistica. Le analisi, presentato in Journal of Complex Networks , ha portato a un'osservazione inaspettata. Si scopre che esiste una somiglianza universale nella struttura dei massicci terrestri. Può essere visto nelle catene montuose di tutti i continenti, indipendentemente dalle dimensioni dei picchi, la loro età, o anche se sono di origine tettonica o vulcanica.
"Sembrerebbe che l'unica cosa che accomuna le varie catene montuose sia che quando le guardi, devi davvero piegare la testa all'indietro. La vera somiglianza diventa visibile solo quando trasformiamo una semplice mappa topografica delle montagne in una mappa di cresta, cioè uno che mostra gli assi di tutte le creste, " dice il dottor Jaroslaw Kwapien (IFJ PAN), e poi aggiunge:"L'asse del crinale è una linea che corre lungo la sommità del crinale della montagna in modo tale che da entrambi i lati il terreno cade verso il basso. È quindi l'opposto dell'asse di una valle".
Le creste montuose non sono creazioni discrete. Si fondono in un grande, struttura ramificata, simile ad un albero:dalla cresta principale ("il tronco") ci sono creste laterali più o meno lunghe del primo ordine ("rami"), da esse sorgono creste laterali del secondo ordine, e da questi successivi ancora e ancora. Il tutto ha una struttura chiaramente gerarchica e il numero dei gradi di complessità dipende dalle dimensioni dell'area ricoperta di montagne e può arrivare anche a diverse decine. Strutture di questo tipo sono presentate sotto forma di vari grafici. Per esempio, ogni cresta di un dato massiccio può essere trattata come un nodo. Due nodi sono collegati da linee (bordi del grafico) quando sono collegate anche le creste corrispondenti. In questo tipo di grafico, alcuni nodi sono collegati a molti nodi, mentre altri sono collegati solo a pochi.
I grafici costruiti per diversi massicci hanno strutture diverse (topologia). Un modo per studiarli è la distribuzione dei gradi dei nodi, contenente informazioni sul numero di nodi di un dato grado. Nelle distribuzioni tipiche, grandi valori appaiono ai nodi di basso grado, perché sono i più numerosi. Di solito non ci sono molti nodi di alto livello:hub. Nel caso delle montagne, il nodo principale, di solito corrispondente alla cresta più lunga della catena montuosa studiata, ha un grado di diverse migliaia. Hub di secondo ordine, cioè creste laterali della cresta principale, avere gradi di diverse centinaia. I più numerosi sono i nodi con grado uno. Ce ne possono essere anche diverse centinaia di migliaia.
"La distribuzione dei gradi dei nodi delle creste risulta essere di natura legge di potenza. Ciò significa che il numero di nodi di un certo grado e, Per esempio, il numero di nodi con grado dimezzato sono in relazione costante, indipendentemente dal titolo di studio prescelto. Ogni frammento della distribuzione aumentato di un certo fattore costante appare come un tutto, il che significa che nessuna scala è distinta, " dice il dottor Kwapien.
Le distribuzioni della legge di potenza si trovano nei grafici che rappresentano i sistemi presenti in natura (ad esempio quando si studiano i legami tra proteine ed enzimi in una cellula vivente), così come nelle nostre attività (come citazioni di articoli scientifici, la collaborazione di attori nei film, la vicinanza delle parole nei testi, collegamenti tra siti web). Spesso descrivono auto-similari, strutture frattali. Uno degli esempi modello di frattali naturali sono le montagne. I loro modelli informatici sono persino generati da algoritmi che utilizzano la geometria frattale, quindi la topologia della legge di potenza dei grafici di cresta non dovrebbe sorprendere nessuno. Però, il valore dell'esponente di potenza si è rivelato una sorpresa.
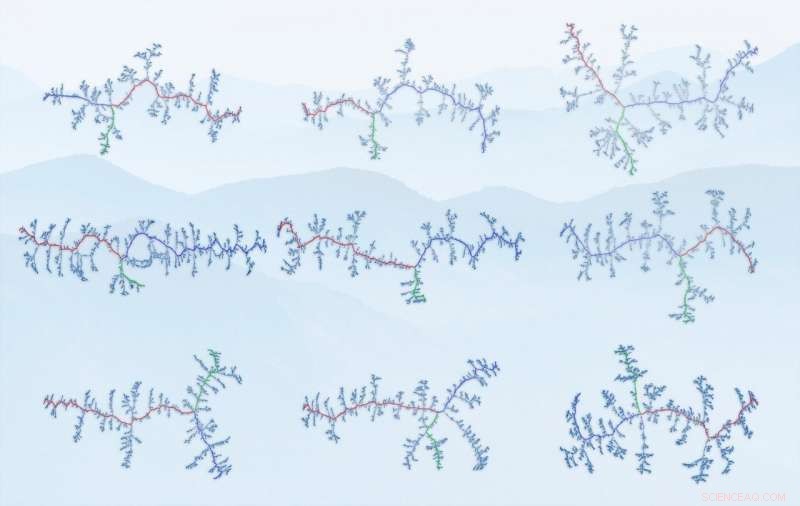
Grafici di cresta delle catene montuose studiate. I nodi qui sono le intersezioni di creste, i bordi - le creste stesse. Da sinistra in alto:Alpi, Monti Betici, Pirenei, montagne scandinave, Himalaya (parte), Alpi meridionali, Monti Appalachi, Ande (parte), Monti dell'Atlante. (Fonte:IFJ PAN) Credito:Fonte:IFJ PAN
"Indipendentemente dal tipo di montagne, l'esponente della distribuzione della legge di potenza ha assunto valori in un intervallo molto ristretto intorno al numero 5/3. Se teniamo conto dell'accuratezza della nostra metodologia, questo ristretto intervallo di valori può anche significare che gli esponenti in ciascun caso esaminato erano gli stessi, " nota il dottor Kwapien.
L'omogeneità osservata deriva dal fatto che in ogni parte del nostro pianeta i principali meccanismi responsabili della scultura di montagna sono sostanzialmente gli stessi. I movimenti tettonici o vulcanici sono necessari per sollevare il terreno, ma il fattore scultoreo più importante è l'acqua e l'erosione glaciale. L'acqua e il ghiaccio provocano la fessurazione e la frantumazione delle rocce e trasferiscono il materiale frammentato nelle pianure. Ciò si traduce in calanchi, canyon e valli montane, e quindi anche creste. Poiché i corsi d'acqua che costituiscono il sistema di drenaggio di una determinata area sono per natura a struttura dendritica (al di fuori delle aree desertiche, Certo), una struttura simile si verifica anche nel caso dei sistemi di colmo. Ma perché le relazioni reciproche tra i numeri di creste con un diverso numero di rami sono così simili per i diversi tipi di montagne?
"La situazione diventa più chiara se consideriamo la gravità oltre all'acqua, " spiega il Dr. Kwapien. "Quando il materiale roccioso viene frantumato, diventa soggetto alla dinamica dei corpi sciolti indipendentemente dalla sua composizione chimica. I corpi sciolti sui pendii possono rimanere lì solo se gli angoli di inclinazione non sono troppo grandi. Le piste non devono essere troppo ripide. Ecco perché la profondità delle valli in natura è limitata dalla loro stessa larghezza. Gli stretti canyon fluviali con pareti quasi verticali esistono solo in una fase iniziale della formazione della scultura. Sono rari nelle formazioni montuose mature perché le loro pareti sono già state inclinate".
L'esistenza di sistemi fluviali che drenano l'acqua da una determinata area, erosione che frantumava rocce e scolpiva valli, così come le frane gravitazionali di detriti rocciosi fanno sì che le creste non possano essere arbitrariamente vicine o lontane l'una dall'altra. C'è una disposizione ottimale, indipendente dalle proprietà della catena montuosa e conferendo alle montagne alcune caratteristiche universali.
Le osservazioni di cui sopra sono integrate da un'altra osservazione fatta dai fisici IFJ PAN, riguardanti le dimensioni delle strutture di cresta frattale. La dimensione frattale descrive quanto sia ruvida la struttura dell'oggetto. La linea di una singola cresta ha dimensione 1. Se le linee (creste) sono state disposte in modo estremamente fitto, la loro dimensione frattale corrisponderebbe alla dimensione della superficie, e quindi sarebbe pari a 2. I ricercatori hanno mostrato che se le strutture di cresta sono presentate come grafici i cui nodi sono le intersezioni delle creste (è in queste intersezioni che i picchi sono più comuni), e i bordi dei grafici sono le creste che collegano i picchi, allora le dimensioni frattali di tali grafici sarebbero con buona approssimazione pari al numero... 5/3.
"In alcuni grafici vediamo la gerarchia delle strutture montane, in altri la loro frattalità. In entrambi i casi, per tutti i tipi di montagne incontriamo gli stessi valori dei numeri appropriati. Questo universalismo dà spunti di riflessione, " afferma il Prof. Stanislaw Drozdz (IFJ PAN, Università della Tecnologia di Cracovia).
Se diverse catene montuose sono così simili in termini di dimensioni, dove sono le fonti della diversità montana? Sarà possibile studiarli usando la teoria dei grafi e la geometria frattale? Sarà possibile creare un modello in cui un grafico in evoluzione imiterà le fasi successive della formazione di una scultura di montagna? Finalmente, sarà possibile applicare in pratica la trasformazione delle mappe di cresta in grafici, per esempio in cartografia? Queste domande, e molte altre, riceveranno risposta solo da ricerche future.