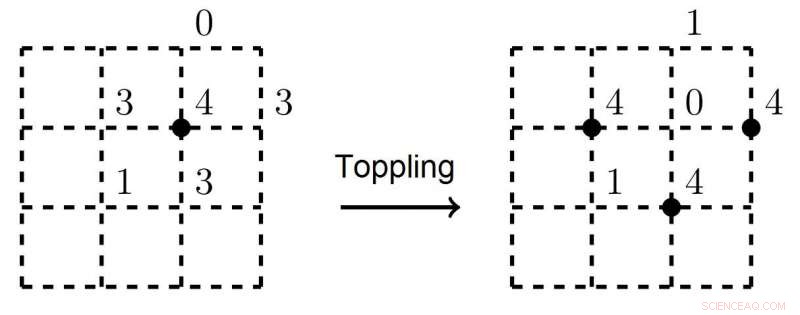
Il punto nero sulla figura a sinistra indica un vertice instabile. Dopo una valanga, tre vertici vicini diventano instabili e collasseranno Credito:Nikita Kalinin, Scuola Superiore di Economia - San Pietroburgo
Un gruppo internazionale di ricercatori (il primo autore è Nikita Kalinin, Higher School of Economics-San Pietroburgo, l'ultimo autore è Ernesto Lupercio, CINVESTAV, Messico) ha presentato il primo modello continuo che descrive le criticità auto-organizzate. La soluzione proposta è più semplice e più universale rispetto al classico modello a catasta di sabbia. Integra aree distanti l'una dall'altra come l'economia, biologia dello sviluppo, e gravità nel contesto della geometria tropicale. Il documento è stato pubblicato in Atti dell'Accademia Nazionale delle Scienze .
Un sistema si dice in uno stato critico se una forza esterna, per quanto piccolo, può produrre un effetto valanga causando un cambiamento nel comportamento del sistema. Questi includono le transizioni di fase:una volta che un singolo cristallo di ghiaccio emerge in acqua raffreddata a zero gradi Celsius, un grappolo di ghiaccio inizierà immediatamente a formarsi.
Ci sono alcuni sistemi dinamici che tendono verso uno stato critico:i terremoti ne sono un esempio illustrativo. Sebbene siano necessarie una certa temperatura e pressione per il congelamento dell'acqua, non è necessario soddisfare parametri precisi perché si verifichi un terremoto. La causa principale dei terremoti è il continuo movimento delle placche tettoniche, e prevedere il momento esatto in cui il sistema raggiungerà uno stato critico e produrrà una valanga è praticamente impossibile.
Molti ricercatori hanno tentato di risolvere il mistero dei terremoti. A metà del XX secolo, I sismologi americani Gutenberg e Richter hanno mostrato una relazione tra la magnitudo e il numero totale di terremoti in una determinata regione. Questa relazione è descritta dalla legge di potenza espressa come una linea retta su una doppia scala logaritmica.
Fenomeni che condividono questa caratteristica sono stati da allora trovati in geofisica, cosmologia, economia, teoria della gestione del rischio e altri campi. Tutti possono essere descritti dalla teoria della criticità auto-organizzata (SOC).
Il concetto di SOC è stato introdotto da Per Bak, Chao Tang e Kurt Wiesenfeld nel 1987. Nel loro articolo fondamentale, propongono l'esempio archetipico di un sistema SOC:il modello Sandpile. Immagina una griglia quadrata con granelli di sabbia in ciascuno dei suoi vertici, in cui nuovi grani cadono sulla griglia con una certa frequenza. Si assume che se non ci sono più di tre granelli di sabbia in ogni vertice, il sistema rimarrà stabile. Ma appena un quarto granello di sabbia cade in cima a un vertice, si rovescia, e la sabbia scivola lungo questo picco e viene ridistribuita ai vertici vicini. Il ribaltamento continuerà in una valanga fino a quando il sistema non tornerà all'equilibrio. La scoperta chiave dei fisici è stata che il numero di vertici che si rovesciano (cioè la dimensione della regione collassata) soddisfa una distribuzione di legge di potenza.
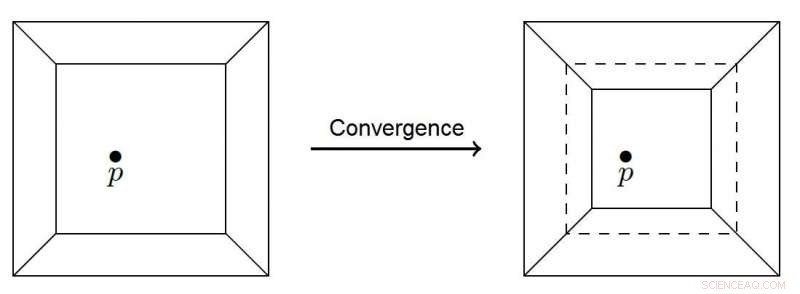
Poligono convergente in un punto. Credito:Nikita Kalinin, Scuola Superiore di Economia - San Pietroburgo
Il modello sandpile è stato a lungo il modello classico che descrive il SOC. Però, descrive la dinamica dei sistemi critici solo a livello fenomenologico e non può essere utilizzata per simulare un terremoto o prevedere il comportamento di un vero e proprio cumulo di sabbia.
"Il vecchio modello di sabbia, essendo puramente combinatoria, si distingue in qualche modo dal grande mondo della matematica. Il nostro modello è un passo avanti, perché ha tutti i vantaggi del modello a catasta di sabbia, ma è anche geometrico e continuo, rendendolo molto più facile da usare, " spiega l'autore Nikita Kalinin, ricercatore senior dell'HSE International Laboratory of Game Theory and Decision Making. "Abbiamo dimostrato che le correlazioni della legge di potenza possono essere ottenute in un sistema continuo che non è un automa cellulare con l'aiuto della geometria tropicale, che ha molte applicazioni oggi."
"La geometria tropicale è una branca della geometria del ventunesimo secolo ispirata alla geometria algebrica classica che è fiorita grazie alle sue connessioni con molti campi della scienza, principalmente teoria delle stringhe, " afferma il Dott. Ernesto Lupercio del CINVESTAV.
Invece della griglia utilizzata nel modello classico della catasta di sabbia, il nuovo modello di pila di sabbia tropicale considera una curva tropicale, un grafico planare con bordi rettilinei, racchiusa in un quadrato. La curva divide il quadrato in regioni poligonali, ciascuno contenente un insieme di punti scelti a caso. Quando viene aggiunto un nuovo punto, la curva tropicale cerca di attraversarla, e la regione poligonale contenente il punto viene accostata mediante un trasferimento parallelo dei suoi bordi. Non appena uno dei bordi raggiunge il punto, il processo si interrompe. Viene quindi aggiunto un nuovo punto, e tutto ricomincia. Il punto precedente potrebbe essere di nuovo fuori curva, e il sistema inizierà a muoversi verso di essa.
Questo processo di convergenza è una variante finita dell'aggiunta di granelli di sabbia a un mucchio di sabbia. Nel nuovo modello, la dimensione della valanga corrisponde all'area spazzata dalle regioni convergenti nel processo avviato con l'aggiunta di un punto casuale. Gli scienziati sperano che il loro modello aiuti a chiarire le relazioni tra i diversi fenomeni che manifestano le proprietà SOC.
"Possiamo osservare somiglianze in diversi fenomeni visti attraverso la lente della matematica. La geometria tropicale ha applicazioni nella teoria delle stringhe, economia e biologia dello sviluppo. Il valore del nostro lavoro sta nel trovare connessioni in luoghi inaspettati. Significa che i metodi applicati a un'area possono essere applicati a un'altra. Hai solo bisogno di fare il passo successivo, "dice Kalinin.